As highlighted by a recent breach, attackers made off with more than $900,000 in crypto due to a flawed key generation mechanism in the Libbitcoin Explorer library. The implications of overlooking the trifecta of random numbers, entropy, and cryptography can be severe.
Aware of the dangers of limited randomness, this article takes a simple approach to explain the basics of entropy in wallet security. Our goal is simple: to clarify the crucial role randomness serves and show how Noone Wallet tackles security from its very foundation.
The Role of Randomness in Private Key Generation
Randomness adds a layer of unpredictability to keep cryptographic operations secure. In transactions, digital signatures act like a seal of authenticity, confirming that a message or transaction is genuine.
To fortify this defense against fraudulent activities, the secret keys involved are generated through a process of deliberate randomness. This randomness ensures that no unauthorized party can anticipate or deduce the keys, thereby safeguarding the integrity and confidentiality of digital interactions.
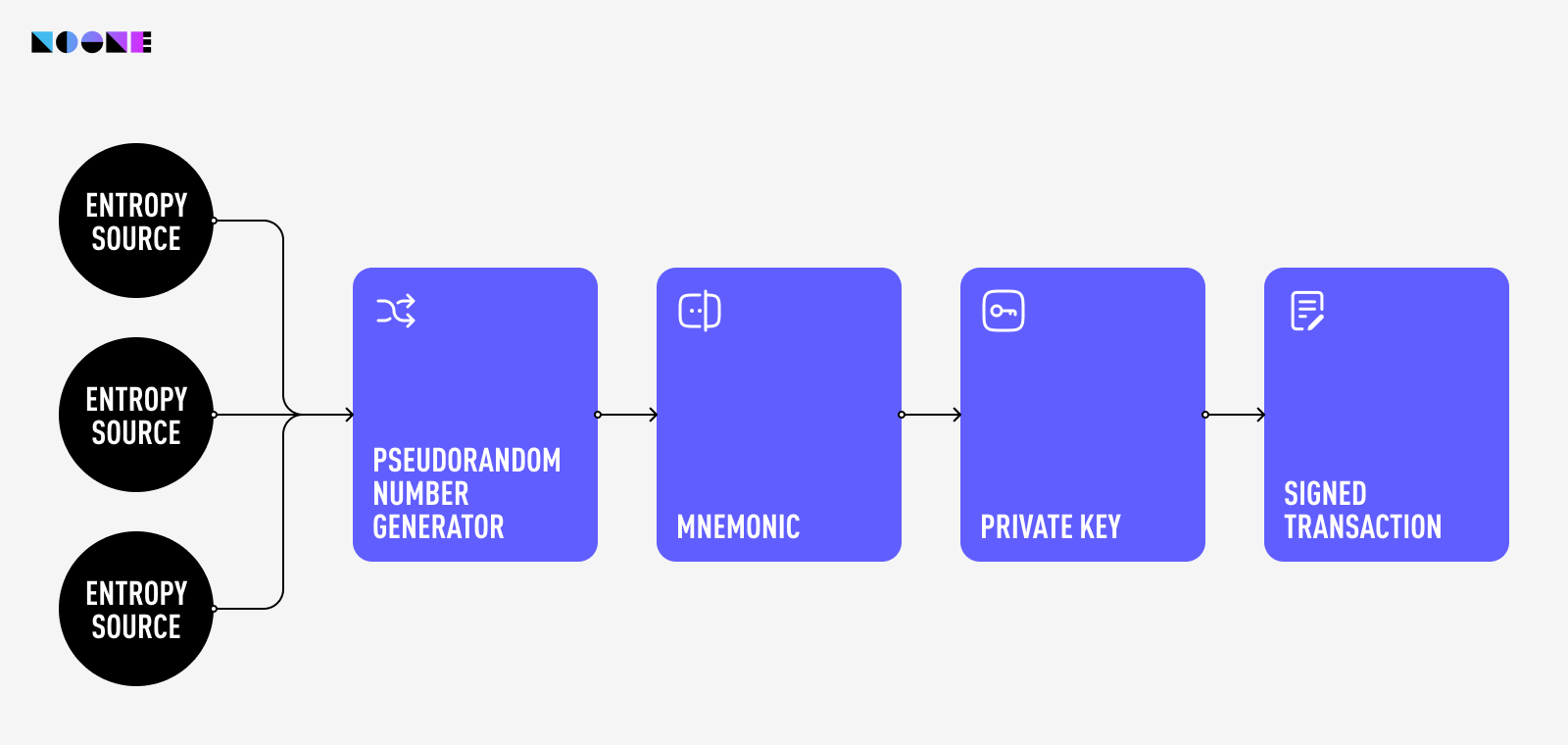
The process of generating a private key is carefully orchestrated through a secure pipeline. This pipeline begins with an entropy source that furnishes randomness. This raw randomness is then channeled into a PseudoRandom Number Generator (PRNG), which in turn produces a stream of random bytes.
These bytes undergo a transformation, culminating in the creation of a mnemonic phrase. From this mnemonic (seed) phrase, the master key is derived. This master private key is then used to generate a hierarchy of other private keys, public keys, and addresses. The private key derived from the seed phrase is the one that controls access to the cryptocurrency funds associated with the wallet.
In both Noone and other contemporary wallets this process is guided by well-established standards such as BIP-32, BIP-39, and BIP-44. BIP-32's hierarchical deterministic wallets (HD wallets) enhance key generation, while BIP-39 simplifies the creation of mnemonic phrases. Simultaneously, BIP-44 establishes a structured hierarchy for key management within these wallets.
Safeguarding Blockchain Through Unpredictability
Consider a twist: envision if this randomization dance could be foreseen, if the machine's inner workings were uncovered. In this scenario, the once-secure wallets become susceptible to attacks. Predictability erodes the very foundation of private key generation. So, how do we reach genuine randomness?
Enter Random Number Generators (RNGs). These algorithms tap into sources like atmospheric noise, temperature fluctuations, or even radioactive decay to produce number sequences that exhibit randomness. Even a coin flip serves as a valid and functional random number generator, just a very slow and inconvenient one because of its restricted range of possible outcomes.

More elaborate methods, such as deriving randomness from unconventional sources like lava lamps, also exist.
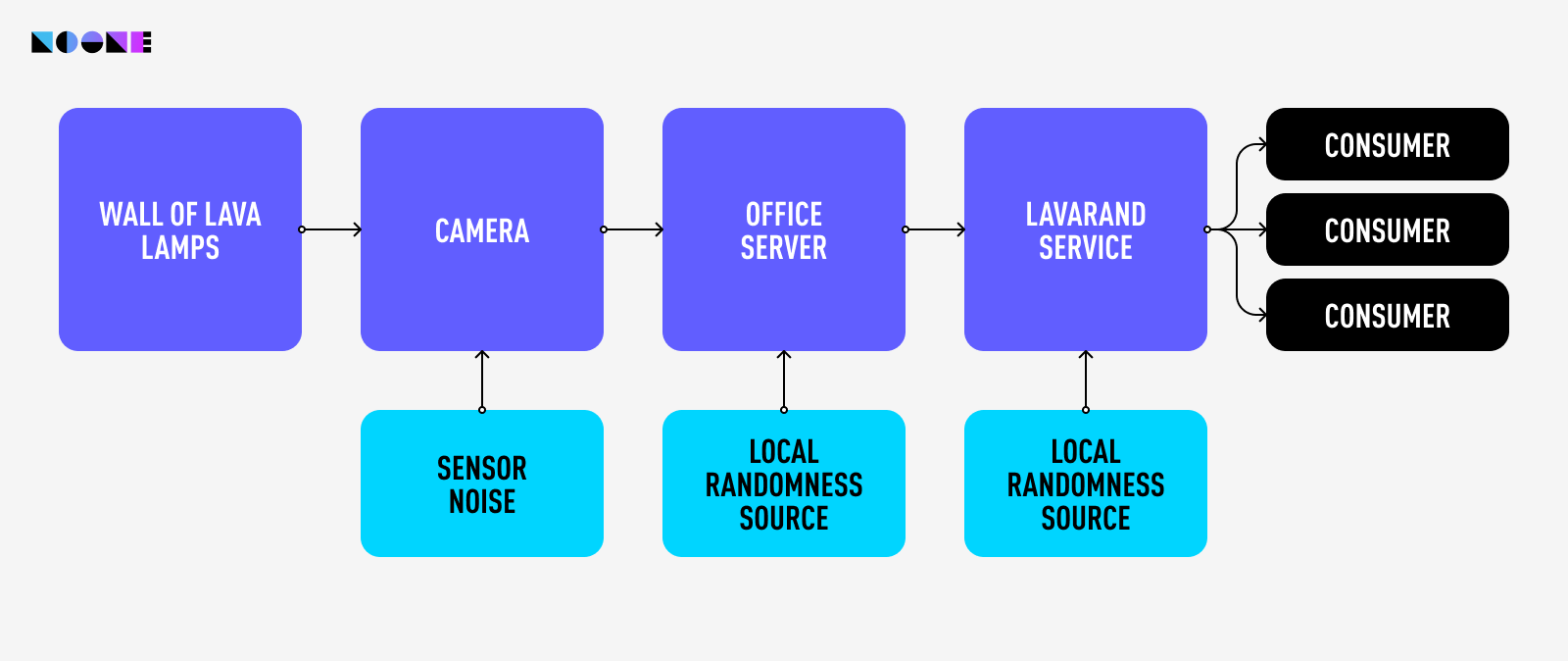
The diagram illustrates Cloudflare's random number generator architecture, highlighting the unique LavaRand setup.
This configuration significantly contributes to the randomness used in Cloudflare's encryption procedures. Since the flow of the “lava” in a lava lamp is very unpredictable, “measuring” the lamps by taking footage of them is a good way to obtain unpredictable randomness.
Beyond this lamp-based source, another originates from a server within the company's premises. Additionally, a data center houses a third randomness source, thereby furnishing Cloudflare with a triad of random number origins. It's worth noting that, while not explicitly mentioned in the scheme, pseudorandom number generators also play a role in this setup.
Pseudorandom Number Generators in Blockchain Security
Despite their potential, true RNGs have limitations. They can be sluggish and resource-intensive, making them less viable for the rapid pace of blockchain transactions.
This is where Pseudorandom Number Generators (PRNGs) step in. PRNGs execute intricate mathematical operations on initial data fragments, crafting an illusion of unpredictability.
Beneath this, however, lies a deterministic core—running the same operation twice yields the same result. Although seemingly deterministic, PRNGs generate sequences statistically indistinguishable from true randomness. PRNGs find use in blockchain technology due to their efficiency and speed—critical traits in the dynamic fintech landscape.
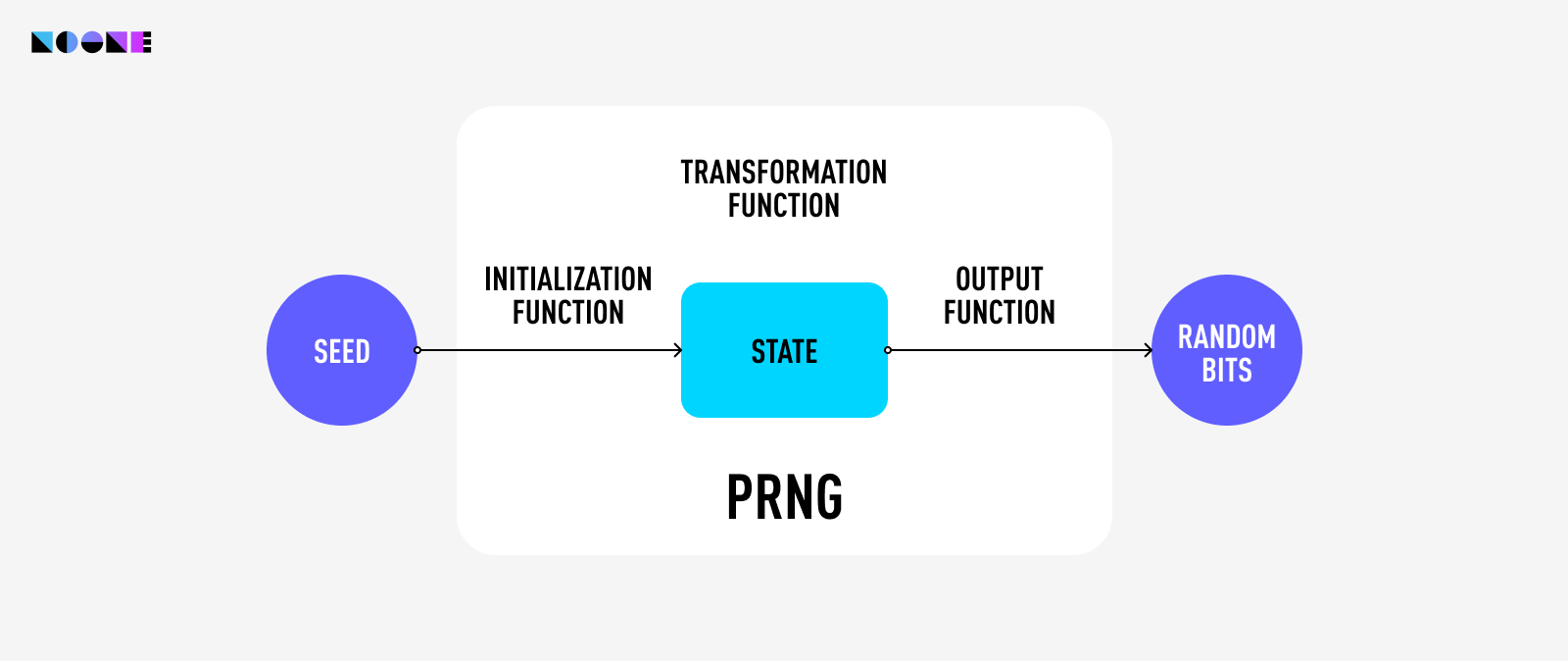
Cryptographically secure PRNGs go beyond just randomness. They must meet certain conditions:
- You can't learn previous random numbers, even if you know any number along the way.
- Even if someone messes with the entropy source, the inner workings of the generator should stay hidden
Entropy's Role in Gauging and Guaranteeing Randomness
Yet, how do we determine if our randomness suffices? We turn to entropy.
Entropy gauges and characterizes the level of randomness in a system. It quantifies how much information is required to describe or predict the outcomes or states of the elements within the system.
NIST (National Institute of Standards and Technology) provides a standardized framework for assessing the quality of entropy sources or random number generators (RNGs). NIST's evaluation involves subjecting the generated sequences to a battery of statistical tests to determine if they exhibit any patterns or deviations from true randomness.
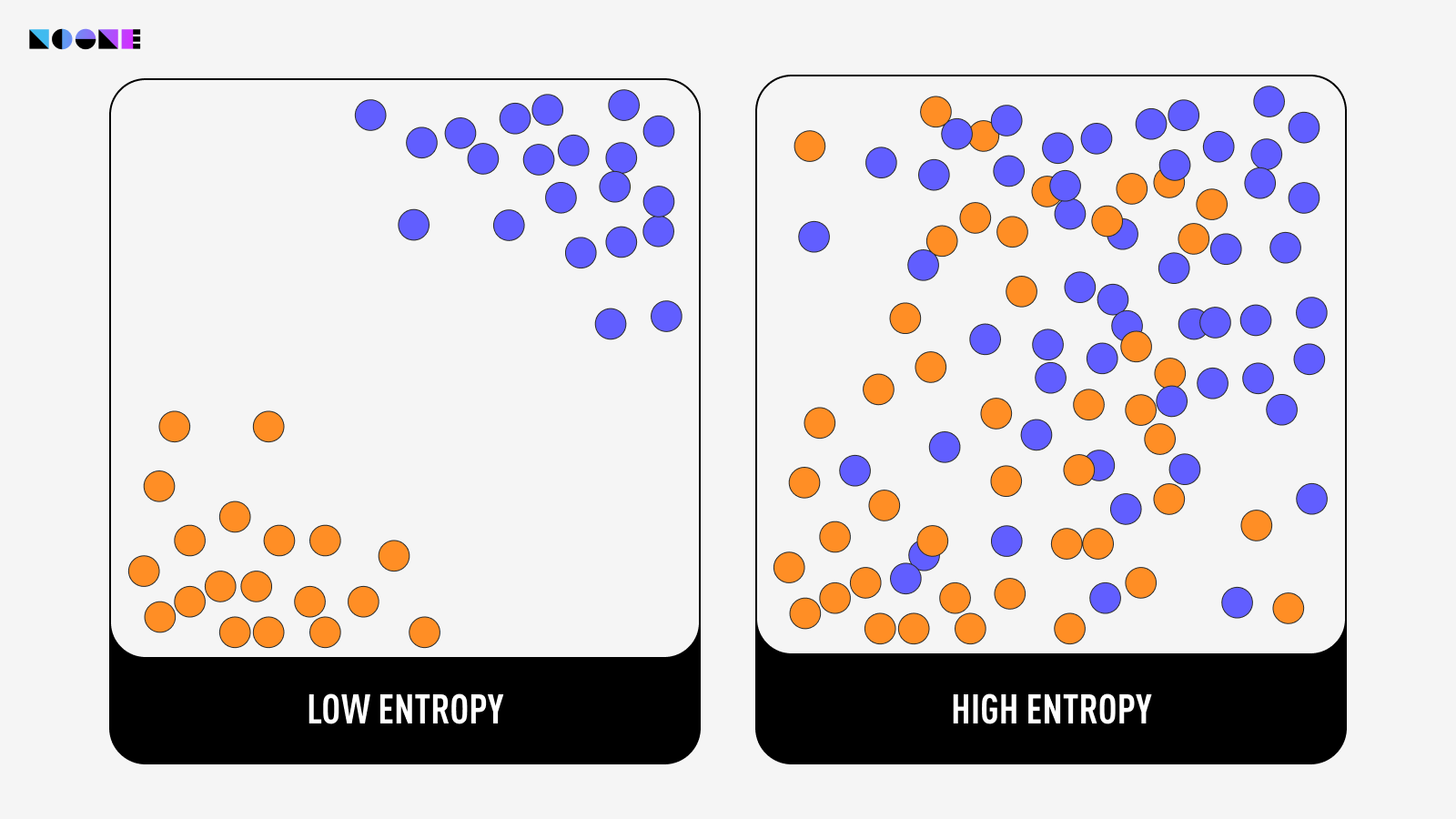
These tests include frequency tests, runs tests, autocorrelation tests, and more. Passing these tests indicates that the sequences have high entropy and demonstrate the characteristics of genuine randomness, making them suitable for applications like cryptography, simulations, and statistical analysis. Many top wallets, including Noone Wallet, have successfully passed these rigorous tests. Feel free to verify our security measures via our open-source core code repository on GitHub.
Measuring Entropy
Entropy is commonly measured in bits due to its direct association with information theory and data representation in binary format. When entropy is quantified in bits, it essentially measures the amount of information required to define or indicate a specific state or result within a system.
For instance, consider a fair coin toss, where the probabilities of getting heads and tails are equal. In this case, one bit of information is sufficient to express the outcome: 0 for heads and 1 for tails.

Familiarity with a value diminishes its entropy—increased understanding correlates with reduced entropy. For instance, a 32-bit random word inherently embodies 32 bits of entropy. If, for example, this word comprises 18 zeros and 14 ones, its entropy diminishes to 28.8 bits.
In the digital realm, computers harvest entropy from embedded sensors. Interrupts, which represent hardware signals directed at the CPU, hold a central role in this symphony of randomness. Every time you press a key, manipulate the mouse, or receive data, these actions set off interrupts, prompting the CPU to take appropriate actions. This data is used to create an "entropy pool", which gradually accumulates random data points over time.
But user inputs are just one facet of the intricate dance of entropy. Hardware events, such as thermal fluctuations and electrical currents, contribute their own element of randomness. Network traffic, with its varying patterns and timing, adds further complexity. Hard drive activities, system clock variations, and even the radio frequency noise emitted by devices all meld into this symphony of unpredictability.
Software typically awaits sufficient entropy accumulation, adhering to established lower entropy flow boundaries. For instance, accelerometers, gyroscopes, and magnetometers contribute about 189 bits/s, 13 bits/s, and 254 bits/s respectively.
Current practice involves reliably sourcing random numbers at the operating system level, subsequently channelled into applications. In the context of the Noone Wallet, the process of generating entropy varies across different platforms.
Challenges in Achieving Genuine Randomness
However, akin to any intricate dance, challenges exist in harnessing entropy's might. While typing on a keyboard or swiping a screen might seem highly random, encryption and security experts offer a different view.
Skilled typists often develop recognizable typing patterns, and the keyboard's scanning rate constrains timing accuracy. Additionally, predicting screen taps is feasible by analyzing the dominant hand's movements. Even attempts to infuse randomness into typed data don't guarantee genuine unpredictability. Hackers can exploit extra cues like keystroke sounds to deduce timing and compromise apparent randomness.
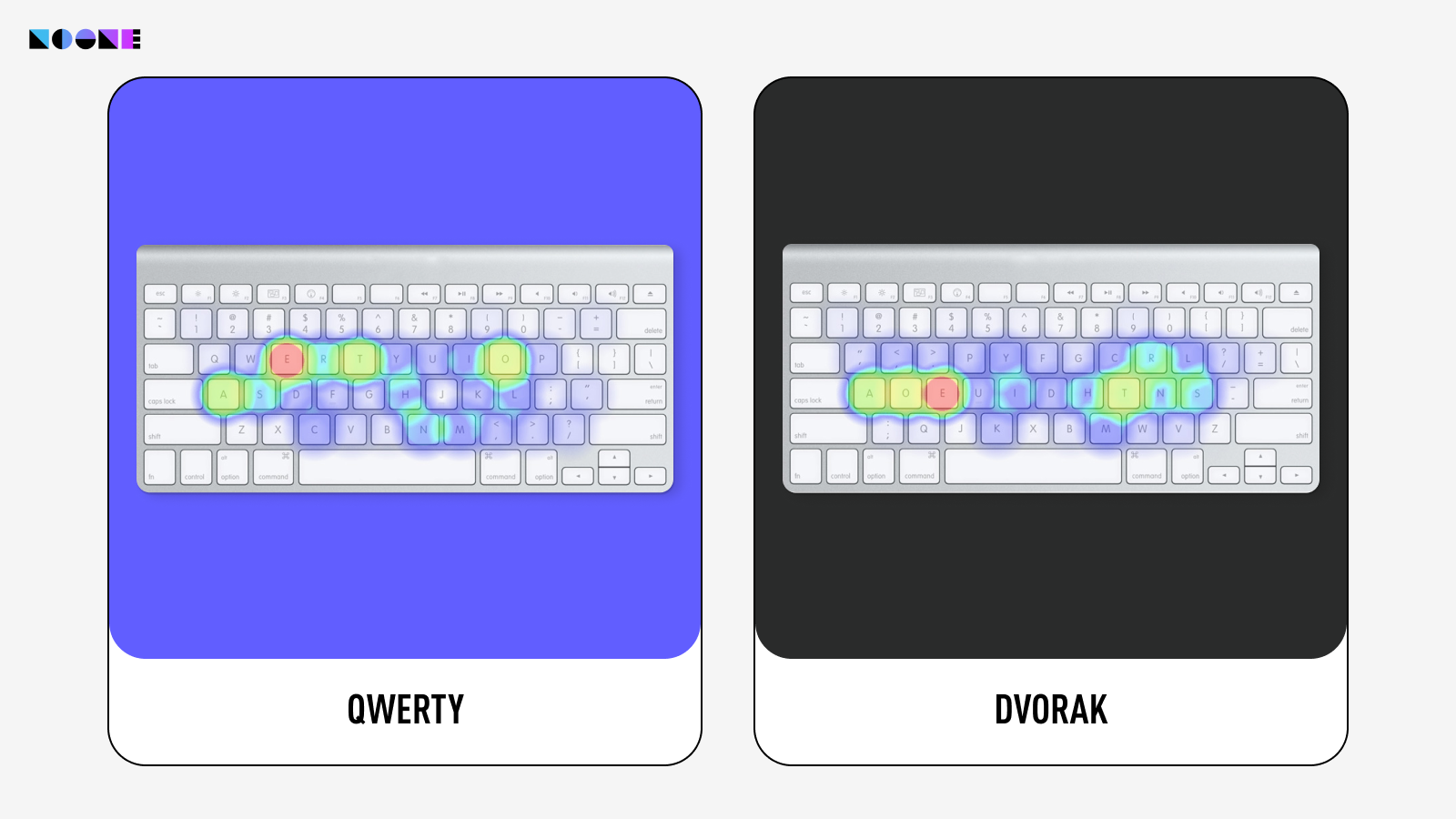
Truly understanding the depth of randomness within our data is a formidable task. Even when we amass random data, more challenges emerge on the road to secure usage:
- Entropy isn't always readily available; actions like keystrokes contribute, yet data-intensive tasks may necessitate waiting.
- Random generators can break and become predictable without clear signs.
- Measuring event-derived randomness is tricky, especially without specialized hardware, complicating accurate assessment.
How Noone Wallet Harnesses Entropy
For Android devices, upon boot-up, the phone collects data from various sources such as interrupts and sensor readings. This collected data is used to create a seed, which serves as the initial input for a secure pseudorandom number generator. When generating encryption keys, the system invokes the SecureRandom function from the Android system library. This function retrieves the necessary bytes from the generated seed to create the encryption keys.
In the case of iOS devices, the secure pseudorandom number generator is initialized when the operating system starts up. This generator continues to supply random numbers throughout the OS's operation. It is also responsible for creating keys within the Noone Wallet. The wallet utilizes a function from the Apple Common Crypto library to access the random numbers provided by this generator.
A comparable process occurs for the web version of the wallet. A random seed is generated during the initialization of the operating system and is periodically updated thereafter. Subsequently, the web browser leverages the crypto.getRandomValues() function to access random numbers. This function operates by utilizing a pseudo-random number generator (PRNG) algorithm, which may differ based on user agents (web browsers). It harnesses the entropy source of the operating system as its PRNG, ensuring a diverse and secure pool of randomness for cryptographic operations.
By employing these methods across different platforms, the Noone Wallet ensures a continuous on-device supply of randomness, which is vital for tasks such as encryption, secure communication, and the reliable unpredictability required by various applications.
From Entropy to Digital Signatures: The Intricate Dance of ECDSA
Now, let's briefly recap before delving into the cryptographic process that safeguards your transactions:
- The unpredictability is collected from sources like mouse movements and keystrokes.
- This reservoir of randomness becomes the foundational input for a cryptographically secure pseudorandom number generator (CSPRNG).
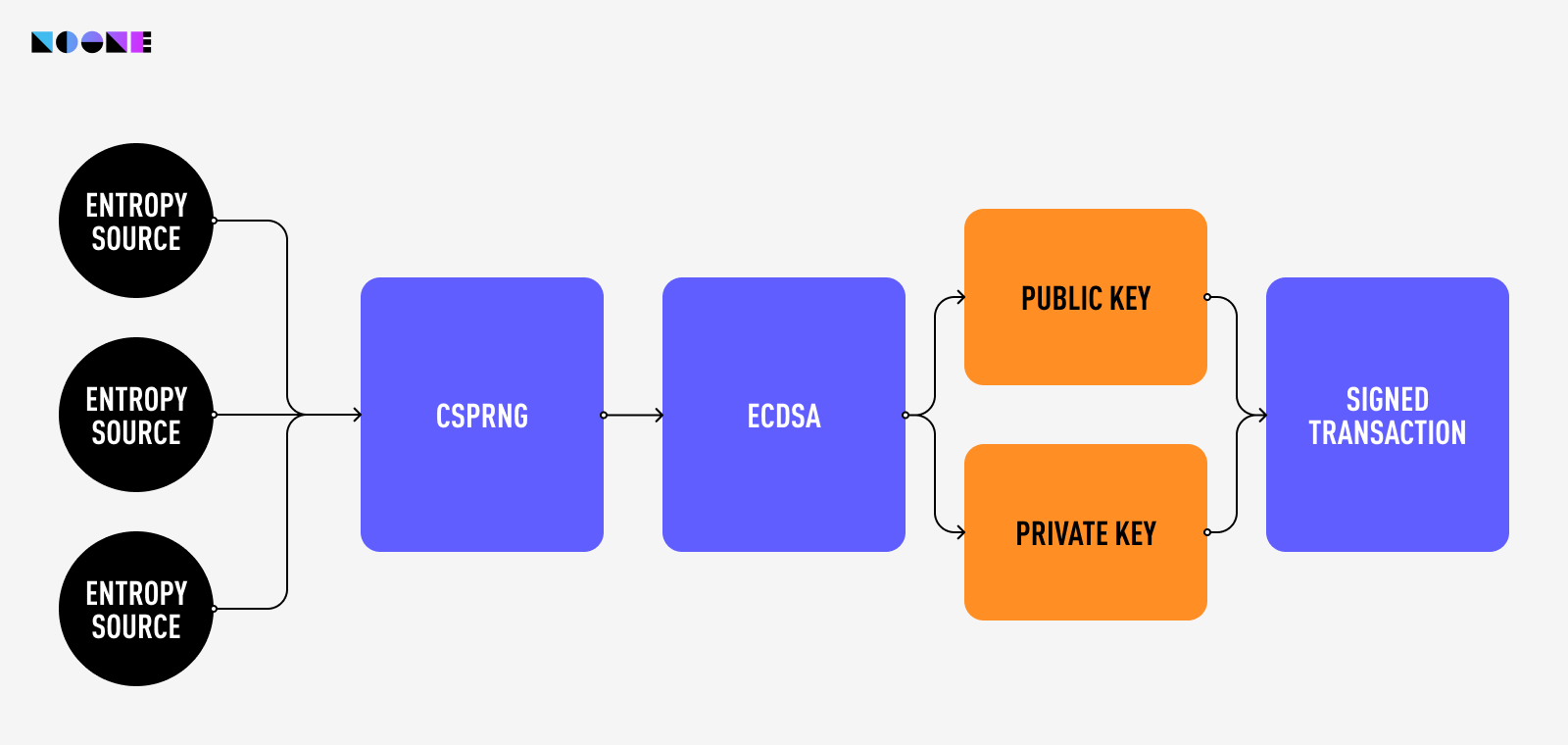
However, these sequences of random numbers are not private keys just yet. This is where the Elliptic Curve Digital Signature Algorithm (ECDSA) comes into play. Its magic lies in its use of elliptic curves, mathematical shapes with special properties. These curves enable ECDSA to create a pair of keys: a private key and a corresponding public key. Think of the public key as a lock and the private key as its unique key.
When you send a transaction, ECDSA uses your private key to generate a digital signature. This signature is like your personal seal, proving that you're the legitimate sender. And because of the special properties of elliptic curves, no one else can create the same signature without your private key.
For 256-bit security, ECDSA requires a 256-bit key, whereas the older Digital Signature Algorithm (DSA) mandates a substantial 3072-bit key.
The inner workings of Elliptic Curve Cryptography (ECC) are detailed and extensive, deserving an article of their own. If you're interested in learning more about ECC, you can refer to this article if you're comfortable with math, or this one if you prefer a simpler explanation.
Summary
Summing it up, our exploration of randomness, entropy, and cryptography offers a glimpse into Noone's security commitment. Equipped with this insight, you can engage with blockchain services fearlessly, confident that your transactions and digital assets are locked behind state-of-the-art security measures.
Unlock the power of Noone White-Label Wallet for your business. Get your own custom crypto wallet today at Noone.io.